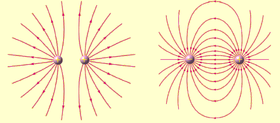
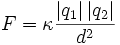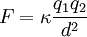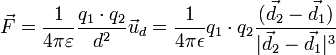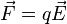La electrostática es la rama de la física que estudia los fenómenos eléctricos producidos por distribuciones de cargas estáticas, esto es, el campo electrostático de un cuerpo cargado.
Históricamente: la electrostática fue la rama del electromagnetismo que primero se desarrolló. Con la postulación de la Ley de Coulomb fue descrita y utilizada en experimentos de laboratorios a partir del siglo XVII, y ya en la segunda mitad del siglo XIX las leyes de Maxwell concluyeron definitivamente su estudio y explicación permitiendo demostrar cómo las leyes de la electrostática y las leyes que gobernaban los fenómenos magnéticos pueden ser estudiados en el mismo marco teórico denominado electromagnetismo.
La existencia del fenómeno electrostático es bien conocido desde la antigüedad, existen numerosos ejemplos ilustrativos que hoy forma parte de la enseñanza moderna; como el de comprobar como ciertos materiales se cargan de electricidad por simple frotadura y atraen, por ejemplo, pequeños trozos de papel o pelo a un globo que previamente se ha frotado con un paño seco.
Alrededor del 600 a. C. el filósofo griego Thales de Mileto describió por primera vez fenómenos electrostáticos producidos al frotar fragmentos de ámbar y comprobar su capacidad de atracción sobre pequeños objetos. Algo más tarde, otro griego, Teofrasto (310 a. C.), realizó un estudio de los diferentes materiales que eran capaces de producir fenómenos eléctricos, escribiendo el primer tratado sobre la electricidad.
A comienzos del siglo XVII comienzan los primeros estudios sobre la electricidad y el magnetismo orientados a mejorar la precisión de la navegación con brújulas magnéticas. El físico real británico William Gilbert utiliza por primera vez la palabra electricidad del griego elektron (ámbar). El jesuita italiano Niccolo Cabeo analizó sus experimentos y fue el primero en comentar que había fuerzas de atracción entre ciertos cuerpos y de repulsión entre otros.
Alrededor de 1672 el físico alemán Otto von Guericke construye la primera máquina electrostática capaz de producir y almacenar energía eléctrica estática por rozamiento. Esta máquina consistía en una bola de azufre atravesada por una varilla que servía para hacer girar la bola. Las manos aplicadas sobre la bola producían una carga mayor que la conseguida hasta entonces. Francis Hawkesbee perfeccionó la máquina de fricción usando una esfera de vidrio hacia 1707.
La electricidad estática es un fenómeno que se debe a una acumulación de cargas eléctricas en un objeto. Esta acumulación puede dar lugar a una descarga eléctrica cuando dicho objeto se pone en contacto con otro.
Antes del año 1832, que fue cuando Michael Faraday publicó los resultados de sus experimentos sobre la identidad de la electricidad, los físicos pensaban que la "electricidad estática" era algo diferente de las otras cargas eléctricas. Michael Faraday demostró que la electricidad inducida desde un imán, la electricidad producida por una batería, y la electricidad estática son todas iguales.
La electricidad estática se produce cuando ciertos materiales se frotan uno contra el otro, como lana contra plástico o las suelas de zapatos contra la alfombra, donde el proceso de frotamiento causa que se retiren los electrones de la superficie de un material y se reubiquen en la superficie del otro material que ofrece niveles energéticos más favorables, o cuando partículas ionizadas se depositan en un material, como por ejemplo, ocurre en los satélites al recibir el flujo del viento solar y de los cinturones de radiación de Van Allen. La capacidad de electrificación de los cuerpos por rozamiento se denomina efecto triboeléctrico, existiendo una clasificación de los distintos materiales denominada secuencia triboeléctrica.